小学数学趣题巧算百题百讲百练--几何部分
有一个直角梯形ABCD,已知AB=8厘米,CD=4厘米,BC=6厘米,三角形ABF的面积比三角形EFD的面积大17.4平方厘米,那么ED长多少厘米?
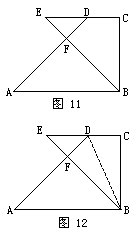
分析与解 连接DB(图12)。已知三角形ABF比三角形EFD的面积大17.4平方厘米,所以三角形ABD比三角形BED的面积也大17.4平方厘米。
三角形BDE的面积是:24-17.4=6.6(平方厘米)。而三角形 BDE的面积等于ED×BC×1/2
即ED×6×1/2=6.6
所以ED长是2.2厘米。
答:ED的长是2.2厘米。
例29 图13由4个正六边形拼成,每个正六边形的面积都是6,那么三角形ABC的面积是多少?
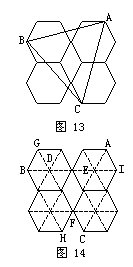
分析与解 首先连接每个正六边形的对角线,将每个六边形平均分成六个小的正三角形(如图14),那么每一个小三角形的面积都是1。
由图14不难看出:三角形ABC是由三角形DEF、三角形AEB、三角形BDC和三角形CFA组成的,其中三角形DEF的面积是4,而其它的三个三角形面积都相等。
先看三角形ABE。它正好是平行四边形AGBE的一半,而平行四边形AGBE的面积是6,因此,三角形ABE的面积是3。当然,三角形BDC和三角形CFA的面积也是3。
由此得出三角形ABC的面积是
4+3×3=13
答:三角形ABC的面积是13。
例30 已知图15中正方形ABCD的面积是256平方厘米,那么正方形EFGH的面积是多少平方厘米?

分析与解 将图15中正方形A0′B′C′D′旋转成图16。由图中不难看出:正方形 A′ B′C′D′的面积是正方形ABCD面积的1/2;正方形EFGH的面积是正方形A′B′C′D′的面积的1/2。因此,正方形
已知正方形ABCD的面积是256平方厘米,所以正方形EFGH的面积是
答:正方形EFGH的面积是64平方厘米。
例31 图17是一个正方形地板砖示意图,在大正方形ABCD中,AA1=AA2=BB1=BB2=CC1=CC2=DD1=DD2,中间小正方形 EFGH的面积是16平方厘米,四块蓝色的三角形的面积总和是72平方厘米,那么大正方形ABCD的面积是多少平方厘米?

分析与解 连AC和BD两条大正方形的对角线,它们相交于O,然后将三角形AOB放在DPC处(如图18和图19)。
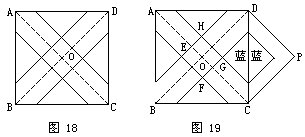
已知小正方形EFGH的面积是16平方厘米,所以小正方形EFGH的边长是4厘米。
又知道四个蓝色的三角形的面积总和是72平方厘米,所以两个蓝色三角形的面积是72÷2=36平方厘米,即图19的正方形OCPD中的小正方形的面积是36平方厘米,那么这个正方形的边长就是6厘米。由此得出,正方形OCPD的边长是4+6=10厘米,当然正方形OCPD的面积就是102,即100平方厘米。而正方形OCPD的面积恰好是正方形ABCD的面积的一半,因此正方形ABCD的面积是200平方厘米。
答:正方形ABCD的面积是200平方厘米。
例32 一个任意凸六边形ABCDEF,P、Q、M、N分别为AB、BC、DE和EF边上的中点。已知阴影部分的面积是100平方厘米,那么六边形ABCDEF的面积是多少平方厘米?

分析与解 连接BF、 BE、 BD,在三角形ABF中,P是AB的中点,那么三角形BPF和三角形APF是等底等高的三角形。因此三角形BPF和三角形APF的面积相等。
同理,由于N为EF中点,所以三角形FNB和三角形 ENB的面积相等;由于M为DE中点,所以三角形DMB和三角形EMB的面积相等;由于Q为BC中点,所以三角形BQD和三角形CQD的面积相等。
由此得出:三角形BPF+三角形BQD+三角形DMB+三角形FNB=三角形APF+三角形CQD+三角形EMB+三角形ENB。
而三角形BPF+三角形BQD+三角形DMB+三角形FNB=阴影面积=100平方厘米,所以三角形APF+三角形CQD+三角形EMB+三角形ENB=空白部分面积=100平方厘米。
因此,六边形 ABCDEF的面积为100×2=200平方厘米。
答:六边形ABCDEF的面积是200平方厘米。
例33 图21是一个圆形钟面,圆周被平均分成了12等份。已知圆形的半径是6厘米,那么图中阴影的面积是多少平方厘米?
分析与解 题中告诉我们:圆周被平均分成了12等份,因此连接OE,
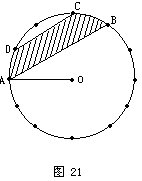
由图中不难看出:三角形AOB与三角形EOB是等底同高的三角形,这两
的面积相等。
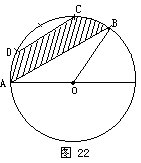
于是图中阴影的面积是:
答:阴影的面积是18.84平方厘米。例34图 23中四边形ABCD是一个正方形。E、F分别为CD和BC边上的中点。已知正方形ABCD的边长是30厘米,那么图中阴影部分的面积是多少平方厘米?
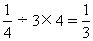
分析与解 已知四边形ABCD为正方形,E、F分别为CD边与BC边上的中点,因此,三角形BCE和三角形DCF面积相等。这两个三角形的面积各自减去四边形GFCE的面积,各自剩下的三角形GBF和三角形GDE面积还是相等的。
连接GC(如图24),三角形GBF面积和三角形GCF的面积是相等的,因为这两个三角形等底同高。同理,三角形GCE面积和三角形GDE的面积也是相等的。而三角形GBF的面积和三角形GDE的面积相等,因此,三角形GBF、三角形GCF、三角形GCE及三角形GDE是具有相等面积的四个三角形。
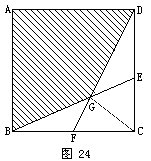
因为三角形BCE的面积等于正方形ABCD面积的1/4,所以图中空白部分的面积,即三角形GBF、三角形GCF、三角形GCE、三角形GDE的面积之和为正方形ABCD面积的
,小学数学趣题巧算百题百讲百练--几何部分- ·上一篇:三位数的读写法
- ·下一篇:小学数学第十二册第二单元试卷(B)
- › 小学数学骨干教师研修总结报告
- › 小学数学课外作业多元化设计探究
- › 第二学期小学数学教研组工作总结
- › 第一学期小学数学教研组工作总结
- › 2016年小学数学教研组工作总结
- › 小学数学集体备课的计划
- › 小学数学教研组学期教学计划
- › 小学数学听课心得
- › 2016年小学数学教师培训心得体会
- › 小学数学三年级下册教学工作总结
- › 参加“全国第九届深化小学数学教学改革观摩交流会”学习心得
- › "小学数学有效课堂教学设计”课题的突破
- 在百度中搜索相关文章:小学数学趣题巧算百题百讲百练--几何部分
tag: 小学数学 小学六年级数学试题,小学六年级数学试题大全,数学教学 - 小学六年级数学试题
相关分类
热门推荐
- · 小学数学毕业模拟试卷(三十六)
- · 小学数学毕业模拟试卷(三十七)
- · 小学数学毕业模拟试卷(三十八)
- · 小学数学毕业模拟试卷(二十五)
- · 小学数学毕业模拟试卷(二十九)
- · 小学数学第十二册第三单元试卷(A)
- · 小学数学趣题巧算百题百讲百练--杂题部
- · 【小学数学解题思路大全】式题的巧解妙算
- · 综合练习九
- · 小学数学三星级看图计算题典型题解
- · 小学数学第十二册第二单元试卷(A)
- · 综合练习七
- · 归一问题
- · 列方程解应用题
- · 小学典型应用题多解详析(三)练习题
- · 巧求面积<练习题>
- · 小学数学解题思路大全【合集】
- · 小学典型应用题多解详析(一)练习题
- · 小学数学三星级计算题典型题库
- · 99年我爱数学少年夏令营数学竞赛试题
- · 简易方程
