小学数学趣题巧算百题百讲百练－－几何部分

   数学网为广大小学生和家长整理的“小学数学趣题巧算百题百讲百练系列”，包括计算、几何、应用题、杂题以及各部分练习题，每部分都有100道精选例题及讲解，以提高广大小学生的综合解题能力。本篇为几何部分。     

   小学生学习几何初步知识，不仅要掌握一些基本的平面图形和立体图形的性质、特征，还要会求这些平面图形的周长、面积及这些立体图形的表面积、体积，而且还要会综合地、巧妙地运用这些知识来进行计算。特别是计算一些组合图形的面积时，常常用到割补、剪拼、平移、翻转等办法，使得计算巧妙、简便。要学会这些方法，应用这些方法。通过解几何题的训练，更好地培养空间想象力，这对学好小学几何初步知识是极有利的，同时也为将来到中学进一步学习几何知识，打下良好而坚实的基础。

　　例21 下图中圆O的面积和长方形OABC的面积相等。已知圆O的周长是9.42厘米，那么长方形OABC的周长是多少厘米？

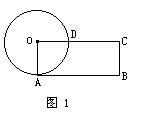
　　分析与解 题中告诉我们，圆O的面积和长方形OABC的面积相等。我们知道，圆的面积等于π·r·r，而图中圆O的半径恰好是长方形的宽，因此长方形OABC的长正好是π·r，即圆O的周长的一半。而长方形的周长等于2个长与2个宽的和，也就是圆O的周长与直径的和。

　　长方形OABC的周长是：

　　9.42+9.42÷3.14

　　=9.42+3

　　=12.42（厘米）

　　答：长方形OABC的周长是12.42厘米。

　　例22 桌面上有一条长80厘米的线段，另外有直径为1厘米、2厘米、3厘米、4厘米、5厘米、8厘米的圆形纸片若干张，现在用这些纸片将桌上线段盖住，并且使所用纸片圆周长总和最短，问这个周长总和是多少厘米？

　　分析与解 要想盖住桌上线段，并且使所用纸片圆周长总和最短，那么盖住线段的圆形纸片应该是互不重叠，一个挨一个地排开，这时若干个圆形纸片直径的总和正好是80厘米。这些圆形纸片周长的总和与直径为80厘米的圆的周长相等，因此盖住桌子上线段的若干个圆形纸片的周长总和是：

　　3.14×80=251.2（厘米）

　　答：这个周长总和是251.2厘米。

　　例23 图2为三个同心圆形的跑道，跑道宽1米。某人沿每条圆形跑道的中间（虚线所示）各跑了1圈，共3圈。他一共跑了多少米？

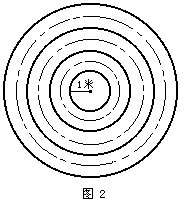
　　分析与解 根据题意，要求某人一共跑了多少米，就是求半径分别为1.5米、2.5米和3.5米的三个圆的周长之和。列式为

　　3.14×（1.5×2）+3.14×（2.5×2）+3.14×（3.5×2）

　　＝3.14×3+3.14×5+3.14×7

　　=3.14×（3+5+7）

　　=3.14×15

　　=47.1（米）

　　还可以这样思考：

　　如果这个人拿着一个1米宽的拖把，边跑边拖地，他跑了1个圆圈，就把这一圈的跑道全拖干净。那么他跑了3个圆圈，就把这三条圆形跑道全拖干净了。他共拖了3个环形面积的地。这3个环形面积的总和是

　　3.14×（42-32）+3.14×（32-22）+3.14×（22-12）

　　=3.14×（42-32+32-22+22-12）

　　=3.14×（42-12）

　　=3.14-[（4+1）×（4-1）]

　　=3.14×15

　　=47.1（平方米）

　　当然，也可以直接列式：3.14×（42-12）=47.1（平方米）

　　因为跑道宽1米，这个人拖完47.1平方米，那么他就前进了47.1米。

　　答：一共跑了47.1米。

　　这里列举的只是某人跑了3个圆形跑道。如果将题改为跑100个这样的圆形跑道，那么用后面介绍的解法计算他跑步的总长度，就简捷多了。

　　解法如下：

　　3.14×（1012-12）

　　=3.14×（101+1）×（101-1）

　　=3.14×102×100

　　=32028（平方米）

　　因为跑道宽1米，所以共跑了32028米。

　　例24 在面积是40平方厘米的正方形中，有一个最大的圆（如图3）。这个圆的面积是多少平方厘米？

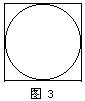
　　分析与解 要求圆的面积，就要先求出圆的半径。题中告诉我们，正方形的面积是40平方厘米，正方形的边长的一半，也就是图中圆的半径。对小学生来讲，从正方形的面积求正方形的边长，还不会直接计算。

　　可以这样思考：

　　把正方形平均分成4份（如图4）。每个小正方形的面积是40÷4=10平方厘米。小正方形的边长恰好是圆的半径，因此圆的半径的平方恰好是10平方厘米。这样就可以求出圆的面积是3.14×10=31.4平方厘米了。

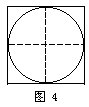
　　答：图中圆面积是31.4平方厘米。

　　例25 图5由正方形ABCD和长方形EFDG部分重叠而成。正方形的边长是247.8厘米；长方形的长是292.404厘米、宽是210厘米，正方形和长方形哪个面积大？

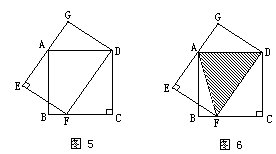
　　分析与解 要比较正方形ABCD和长方形EFDG面积的大小，方法是分别算出它们的面积再进行比较。从题中给出的数据看，确实给计算带来麻烦。

　　只要在AF两点间连一条线段（如图6），就会发现，三角形 AFD的面积是正方形 ABCD面积的一半，同时也是长方形EFDG面积的一半，所以正方形ABCD和长方形EFDG的面积一样大。这样，也就不用计算这两个图形的面积了。

　　例26 图7由半圆和等腰直角三角形重叠而成。已知等腰直角三角形的直角边长为4厘米，求图中阴影面积。

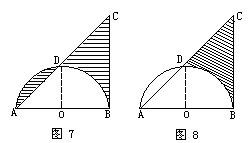
　　分析与解 如果分别算出两个阴影部分的面积，再把它们加起来，以便求出图中阴影部分的总面积，那就太复杂了。

　　根据题中的条件，我们可以把图中弓形阴影剪下来拼（或旋转）成图8。

　　从图8不难看出，题中要求的阴影部分的面积就是三角形 ABC面积的一半。

　　图中的阴影面积是：

　　（4×4÷2）÷2=4（平方厘米）

　　答：图中阴影面积是4平方厘米。

　　例27 有5个正方形（如图9），边长分别是1米、2米、3米、4米、5米。问图中白色部分面积与阴影部分面积的比是几比几？

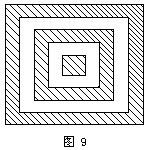
　　分析与解 观察已知图形，显然，先计算出白色面积比较简单。

　　白色部分面积是：（22-12）+（42-32）=10（平方米）

　　阴影部分面积是：52-10=15（平方米）

　　因此，白色部分面积与阴影部分面积之比是：10∶15，即2∶3。

　　还可以这样想：作正方形的对角线AD和BC，两条对角线相交于O，于是两条对角线把正方形平均分成四部分（如图10）。

　　要计算整个图形中白色部分面积与阴影部分面积的比，只需计算三角形AOB中白色部分面积与阴影部分面积的比就可以了。在三角形AOB中，可把白色的和阴影的两部分图形都看作是一些梯形，其中把最上端的小阴影三角形看作是上底为O的梯形。这些梯形的高都相等，所以这些梯形面积之比就是这些梯形上、下底的和之比。

　　从小到大，5个梯形面积比是：

　　1∶（1+2）∶（2+3）

　　∶（3+4）∶（4+5）=1∶3∶5∶7∶9

　　因此，图中白色部分面积与阴影部分面积的比是：（3+7）∶（1+5+9）=2∶3

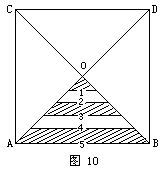
　　答：图中白色部分面积与阴影部分面积比是2∶3。

　　例28

[1] [2] [3] [4]  下一页